La meccanica del lancio: La Lenza
Graig A. Spolek
Professore Associato, Dipartimento di Ingegneria Meccanica,
Portland State University, P.O. B751, Portland, Oregon 97207.
(Ricevuto il 25 Febbraio 1985; accettato per la pubblicazione il 10 settembre 1985)
Traduzione Barbara Panizzolo
Al fine di spingere una mosca attraverso l’aria verso la distante preda, una lenza piuttosto massiccia, a cui la mosca è attaccata, è il lancio. Quando la lenza si srotola,la mosca accelera effettivamente in orizzontale e sembra sfidare la legge fisica. Il fenomeno è modellato per semplicità per determinare l’importanza di questo effetto. In assenza della resistenza dell’aria , la mosca può accelerare per aumentare la sua velocità con un ordine di grandezza. La frizione diminuisce di molto l’effetto, ma un’accelerazione della mosca è ancora prevista. Con l’affusolamento della lenza in diversi modi, l’andamento della velocità della mosca può essere modificata significativamente, ed è previsto che alcune rastremazioni siano più performanti di altre.
I.INTRODUZIONE
In molte attività ricreative si richiede al partecipante di lanciare un oggetto o per distanza, per precisione, o entrambe; esempi di questi oggetti sono il baseball, il giavellotto, la pallottola del fucile, la palla da golf, il saltatore con gli sci, il disco e la freccia. Da quando l’oggetto è lanciato con velocità e direzione iniziali, le uniche forze maggiori che riguardano il suo percorso di movimento sono la forza del corpo dovuta alla gravità e la frizione dell’aria o attrito viscoso. Il molti casi, il fattore che limita la prestazione è l’attrito dell’aria. La sua minimizzazione è l’obiettivo della tecnica fisica e del design dell’attrezzatura. Come esempi, il saltatore con gli sci si sforza per mantenere l’orientazione aerodinamica degli sci e del corpo, ed una pallina da golf è dotata di fossette per causare lo strato limite dell’aria per viaggiare da laminare a turbolento per ridurre il coefficiente di resistenza. In tutti i casi, comunque, l’attrito dell’aria diminuisce la componente orizzontale della velocità dell’oggetto attraverso il suo volo.
Il lancio nella pesca con esche artificiali è abbastanza simile al lancio di oggetti appena descritto eccetto una forza addizionale che agisce sull’esca artificiale. L’esca è legata al lanciatore attraverso la lenza, apparentemente per consentire al pescatore di avvolgere il pesce ma più realisticamente per consentire il recupero dell’esca vuota. Quando l’esca è lanciata con l’aiuto della canna da pesca, il moto dell’esca è frenato dall’attrito dell’aria ed è anche ritardato dalla forza necessaria a far allentare la lenza. Dunque, la sua velocità orizzontale diminuisce con un tasso più alto di quello che si avrebbe nel volo libero. È facile visualizzare che così come l’esca diventa progressivamente più leggera con un grande coefficiente di attrito, sarà virtualmente impossibile lanciarla come un proiettile per una distanza utile. Questo è precisamente il problema che affronta il pescatore che utilizza mosche artificiali come esche.
Le mosche per la pesca sono disegnate per imitare gli insetti che galleggiano. Essi sono molto leggeri con un volume relativamente grande di piume e pellicce così la tensione superficiale che si esercita sulla vasta area della superficie può far galleggiare la mosca. A causa della grande superficie, il moto della mosca durante un lancio è facilmente dominato dall’attrito dell’aria. Per esempio,per lanciare una tipica mosca orizzontalmente a 20m da un’altezza di 1.5 m, senza nemmeno alcuna lenza attaccata ad essa, sarebbe richiesta una velocità iniziale in eccesso di 140 m/s (313 mph), una condizione quindi proibitiva.
La soluzione per il dilemma di chi pesca con la mosca è quella di lanciare una lenza abbastanza massiccia a cui è attaccata la mosca e che consenta alla mosca di andare avanti per il giro. Come risultato di questa relazione simbolica tra la lenza e la mosca, la mosca (come l’oggetto lanciato) dimostra un comportamento durante il volo che è unico rispetto agli altri:accelera in orizzontale. Mentre questo effetto può essere intuitivamente sconcertante, i fisici che prevedono l’effetto sono abbastanza ottimisti.
L’intento di questo documento è quello di studiare l’accelerazione del lancio con la mosca e di esaminare i parametri che influenzano la sua grandezza. Un semplice modello di lancio con la mosca è stato sviluppato, e le equazioni sono state risolte numericamente per predire la’andamento della velocità della mosca. Questi sono i fattori specifici analizzati
(1)Quanto varia la velocità della mosca durante il moto in assenza dell’attrito dell’aria?
(2)Qual è l’effetto dell’attrito dell’aria sull’ andamento della velocità?
(3)Come l’affusolamento della lenza,come è comunemente fatto con le code disponibili in commercio, influenza la velocità della mosca?
II. SFONDO
Secondo la conoscenza dell’autore, non ci sono stati studi precedenti della meccanica della mosca e della lenza durante un lancio. Altri autori hanno discusso la meccanica di un lancio con la mosca,ma si sono concentrati sull’interazione tra la canna e la lenza fino a quando la velocità di lancio è stata raggiunta.1-3 Questo studio,in contrasto, esaminerà il comportamento della lenza da questo punto in avanti. Un altro documento4 ha esaminato la meccanica del leader, che si comporta in modo simile alla lenza, durante un tipico lancio. Comunque, quello studio ha assunto l’andamento della velocità per il leader piuttosto che risolverla partendo dall’equazione lavoro-energia. Il lancio della lenza è analogo per molti aspetti alla rottura di una frusta, e sono stati riportati due studi 5,6 che analizzano l’andamento della velocità per la punta di quel dispositivo. Nessuna delle analisi menzionate include gli effetti viscosi dell’aria.
III: MODELLO
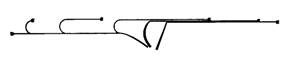
I pescatori con la mosca usano una grande varietà di lanci che dipendono dalle condizioni di pesca e dalle loro attrezzature. Tra questa moltitudine di lanci, probabilmente il più comune è il lancio sopra la testa. Ai fini di questo studio, sarà modellato un lancio sopra la testa senza alcun aumento nella lunghezza della lenza. Per riprodurre questo lancio, il pescatore fa allentare la lenza fino alla lunghezza desiderata con un falso lancio in cui la mosca non può toccare l’acqua. Un lancio all’indietro è poi eseguito per estendere l’intera lenza dietro al pescatore. L’analisi del lancio inizierà quando la lenza sarà interamente estesa dietro al pescatore come illustrato in Figura 1. Con la lenza inizialmente dritta nel lancio all’indietro, il pescatore applica forza e momento torcente alla base della canna per causare il rovesciamento della canna ed attacca la lenza per accelerare. Quando la canna si raddrizza e poi inizia a flettersi in avanti, la velocità della punta della canna diminuisce e la lenza viaggia libera dal moto della canna.
Fig 1 il moto della lenza durante il ancio sopra la testa
La velocità orizzontale della lenza equivale alla massima componente della velocità della punta della canna. Comunque, dal momento che la fine della lenza è attaccata alla punta della canna, quell’estremità avrà essenzialmente velocità uguale a zero. Così, la lenza attaccata è stazionaria mentre la lenza rimanente si sta spostando, ed il loop si è formato aull’interfaccia tra questi due segmenti di lenza. Dal momento che la lunghezza relativa di ogni porzione di lenza varierà durante il lancio, il loop si sposterà lungo la lenza come un’onda fino a quando raggiunge l’estremità libera della lenza portando la mosca. Il loop si srotola, la lenza si raddrizza, ed il lancio è completo.
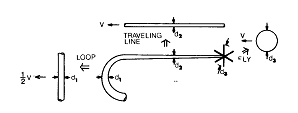
Il metodo lavoro-energia è impiegato per determinare la velocità della lenza che si sposta e della mosca attaccata. La nomenclatura e le variabili nel modello sono illustrate in Fig. 2. Il lancio inizia con un loop di diametro D, lunghezza iniziale della lenza L0 massa iniziale m0 e velocità iniziale V0. In assenza di attrito viscoso, la conservazione dell’energia cinetica prevede la velocità della lenza che si sposta in tutti gli istanti di tempo t come:
(1/2)m(t)V(t)2 = (1/2)m0V02 (1)
La massa della lenza che si sposta m(t) diminuirà con il progredire del lancio e da quando L(t) diminuisce. La semplice relazione
m(t) = rL(t) (2)
dove r è la massa della lenza per unità di lunghezza, può essere usata per prevedere m(t) se la lenza ha diametro uniforme. Le lenze di seta usate per anni dai pescatori sono quasi di diametro uniforme e sarebbero giuste per questo modello. Ma la moderna tecnologia dei polimeri ha prodotto lenze che hanno varie sezioni affusolate lungo la loro lunghezza. Queste lenze sono usate dalla maggior parte dei pescatori per costo e prestazioni. Per queste lenze affusolate, il volume della linea in movimento deve essere calcolato e deve essere utilizzata la densità della lenza. E’ anche da notare che la massa della mosca mf, che è piccola ma finita, deve essere aggiunta in modo che
m(t) = rL(t) + mf (3)
Gli effetti dell’attrito dell’aria non sono trascurabili e devono essere inclusi. Dato che l’attrito viscoso è dissipativi,l’energia cinetica della lenza durante un lancio diminuirà di continuo come il lavoro che è fatto dalla lenza sull’aria circostante. Quindi, l’equazione lavoro-energia per la lenza è
(1/2)m(t)V(t)2 = (1/2)m0V02 – ò0S(t) F(t)ds (4)
–
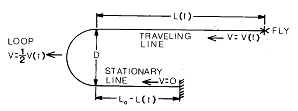
Fig.2 Nomenclatura del modello della lenza.
–
–
–
Fig. 3Lenza semplificata per il calcolo dell’attrito
_
_
–
Anche
Ds = V(t)dt (5)
S(t) = òV(t)dt (6)
L(t) = (1/2)S(t) (7)
La forza d’attrito F(t) che agisce sulla lenza può essere scritta come
F(t) = å [(CDA)i(1/2)raV(t)i2] (8)
Dove si assume che il sistema lenza/mosca può essere separato in n distinti segmenti. Poi per ciascun segmento i, CD è il coefficiente di attrito, A è l’area della superficie caratteristica, V(t) è la velocità istantanea (assumendo come velocità zero l’aria circostante), e ra è la densità dell’aria. Le parti maggiormente distinguibili della lenza lanciata che contribuiscono all’attrito viscoso sono il loop, la lenza in movimento e la mosca. Alcune assunzioni semplificate sono necessarie per ognuna di queste parti per consentire il calcolo dei coefficienti di attrito rappresentativo e delle aree di superficie. L’essenza di ciascuna assunzione è illustrata in Fig 3dove una lenza affusolata è modellata per indicare il diametro effettivo utilizzato per ciascun segmento .
Il Loop è modellato come un cilindro uniforme a flusso incrociato con lunghezza equivalente al diametro del loop e diametro del cilindro equivalente al diametro medio dell’affusolamento contenuto nel loop. Il coefficiente di attrito per un cilindro a flusso incrociato è approssimativamente costante e vale 1.0 nell’intervallo dei numeri di Reynolds che serve in questo modello. La velocità del loop è uguale alla metà di quella della lenza che si sta spostando,quindi
Vloop= (1/2) V(t) (9)
Il modello del loop che rotola come un cilindro a flusso incrociato è una maggiore semplificazione ma è impiegato per la mancanza di un modello più significativo. Come è dimostrato più tardi, l’attrito dell’aria sul loop domina l’effetto viscoso totale, perciò questo aspetto del modello può senza dubbio apportare benefici per raffinatezza.
La lenza in movimento è modellata come un lungo cilindro parallelo alla corrente, e la correlazione del coefficiente d’attrito consigliata da White7 per questa condizione è
CD = 0.0015 + [0.30 + 0.015(L/r)0.4]ReL-1/3 (10)
Il diametro medio della rastremazione della lenza che si sposta è utilizzato per calcolare il rapporto L/r così come l’area superficiale della lenza.
La mosca è modellata come una sfera con diametro effettivo di 1.5cm che è rappresentativo di una mosca tipicamente folta ed asciutta.
Nell’intervallo dei numeri di Reynods che si applica alla mosca, il coefficiente d’attrito per una sfera è abbastanza costante e CD = 0.4 e qui applichiamo questo. L’attrito della mosca dimostra di dare un piccolo contributo all’attrito complessivo, per questo le in accuratezza su queste approssimazioni non sono severe.
Combinando le equaizoni (3) – (10), l’approccio lavoro-energia produce una singola equazione non lineare differenziale per la velocità istantanea della mosca e per la porzione della lenza che si sposta. L’equazione è stata risolta numericamente, usando un’integrazione mista esplicita ed implicita nel tempo per aumentare la stabilità della soluzione. Le condizioni iniziali richieste per iniziare il calcolo sono la massa iniziale e la velocità. I valori richiesti per determinare la massa sono la massa della mosca , la lunghezza iniziale della lenza che si muove la sua rastremazione e la densità della lenza. Il diametro del loop è anche inserito come quantità indipendente. La velocità è calcolata per ogni incremento di tempo, e lo spostamento integrato della mosca è dato per consentire la presa in esame dell’andamento spaziale della velocità della mosca V(S)). In questo modo, gli effetti parametrici sulla lunghezza del lancio dato possono essere comparati.
IV. RISULTATI
La prestazione di un lancio standard sono state calcolate prima. Tutte le variazioni parametriche sono state poi comparate con questo standard. Le caratteristiche di questo lancio standard sono come segue:
(1) Lunghezza iniziale della lenza = 20 m. Questa è anche la lunghezza del lancio, o la distanza del pescatore dal pesce. Questa distanza sarebbe considerata abbastanza lunga per questo tipo i lancio. (2)Diametro del loop = 1 m. Questo diametro del loop è tipico del lanciatore medio; i bravi lanciatori lanciano loop più stretti mentre i lanciatori meno esperti lanciano loop più grandi. (3)Velocità finale della mosca = 30 m/s. Questa è la velocità della mosca prima dello srotolamento del loop del capo ed è alquanto arbitrario, dal momento che non è disponibile alcun dato. È stato scelto di rappresentare ila peggiore condizione per la necessaria veloci tà iniziale orizzontale della mosca per permetterle di viaggiare in orizzontale per 6 m (due volte la lunghezza del capo) mentre cade di 1metro (diametro del loop). Solo l’attrito dell’aria e la gravità hanno agito sulla mosca durante il suo volo, richiedendo un capo privo di massa (4) Proprietà della Lenza. Gravità specifica della lenza = 0.8,utilizzando una tipica lenza galleggiante. La massa della lenza varia ma i primi 9.14m (30 piedi) di ciascuna linea devono avere una massa di 12g(185 grani), che è lo standard industriale per una lenza N. 7 (5) Rastremazioni della lenza. Ci si è interrogati su molte tipologie di rastremazione della lenza: (A) Livello (L). Una lenza disponibile in commercio , questa lenza ha un diametro uniforme lungo tutta la sua lunghezza. (B) Doppia rastremazione (DT). Una lenza disponibile in commercio che è una delle lenze più conosciute per questo tipo di lancio. Ogni estremo di questa lenza ha una rastremazione composta che consiste di 0.61 m (2 piedi) della lenza di livello, seguita da 3.05 m(10piedi) di lenza con diametro che si allarga seguita da una porzione centrale di lenza di livello. È lanciata solo un’estremità mentre l’altra resta sul mulinello. (C)Lunga Rastremazione(LT). Questa lenza esiste solo nella mente di questo autore, che consiste in un diametro uniformemente in crescita attraverso la sua lunghezza,che inizia con lo stesso diametro della punta come la lenza commerciale doppiamente rastremata. Questa rastremazione simula una frusta. (D) Rastremazione sperimentale (ET). Anche questa è una lenza inventata per motivi di analisi. Si rende anche conica per aumentare il diametro uniformemente attraverso la sua lunghezza come la lunga lenza conica, ma la rastremazione è meno marcata. Il diametro della punta è selezionato per generare un comportamento molto specifico che è dimostrato dopo.
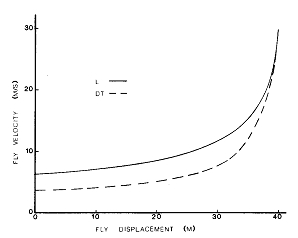
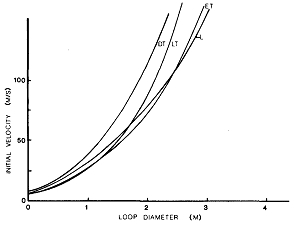
Dato che il lancio è lungo 20 metri in ogni caso, la mosca deve viaggiare per una distanza di 40m. Se gli effetti dell’attrito dell’aria sono ignorati, la velocità della mosca aumenta continuamente lungo il suo cammino come dimostrato in Fig 4. Per la lenza di livello, per esempio, una velocità di circa 6 m/s è richiesta per produrre i desiderati 30 m/s per il completamento del lancio.
Fig. 4 Andamento della velocità della mosca senza attrito dell’aria.
Il rapporto di queste velocità, come indicazione di accelerazione della lenza, sarebbe migliore se il completamento del lancio non includesse la massa della lenza nel loop che si sposta alla velocità del loop stesso.
Dato che le lenze coniche hanno un diametro più piccolo sulla punta, quindi meno massa nei loro rispettivi loops, essi dimostrano un aumento più marcato della velocità rispetto a quanto faccia la lenza di livello. In ogni caso , il calcolo senza attrito viscoso mostra che la mosca accelera durante un lancio.
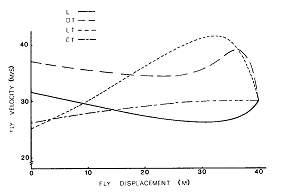
La viscosità dell’aria ha effetti molto interessanti sulla velocità della mosca durante il suo volo; queste sono mostrate in Fig. 5. Di nuovo, la velocità finale per ogni lenza era fissata a 30 m/s, mentre sono richieste velocità iniziali molto differenti. In generale, tutte le lenze dimostrano andamenti della velocità molto più uniformi delle controparti non viscose, con molta meno accelerazione. La lenza di livello rallenta lungo la maggior parte del suo viaggio, e poi accelera solo alla fine del lancio. Questo comportamento è necessario perché il lavoro viscoso per la lunga lenza che si muove è migliore del corrispondente aumento di velocità dovuto alla diminuzione della massa. Solo se la massa della lenza che si sposta diventa abbastanza piccola la massa relativa cambia sopraffacendo l’effetto viscoso.
La lunga lenza a cono mostra solo l’andamento opposto della lenza di livello della Fif 5. Questa lenza continua ad accelerare con il progredire del lancio e poi decelera rapidamente al completamento del lancio.
Fig 5 Andamento della velocità della mosca con attrito dell’aria.
Per la lunga lenza conica, il diametro decrescente della lenza migliora il tasso di diminuzione della massa sulla lenza che si muove. Gli effetti inerziali dominano gli effetti viscosi fino a che il diametro della lenza diventa piccolo abbastanza, in quell’istante gli effetti viscosi prendono il loro posto per fare decelerare la mosca. Dato che la pendenza di decelerazione è così ripida,piccole variazioni nella tecnica di lancio possono dimostrare un impatto drastico sulla velocità della mosca.
Nello sforzo di dissociare la velocità finale della mosca dalla tecnica di lancio, fu progettata la conicità sperimentale. Dato che la lenza di livello accelera e la lunga lenza rastremata decelera al completamento del lancio, deve esistere una lenza intermedia che dimostri una velocità costante al completamento del lancio. Ciò, infatti, è vero ed è dimostrato dalla curva per il cono sperimentale in Fig, 5. Teoricamente, questa lenza dovrebbe lanciare in modo più consistente di quelle precedentemente discusse.
Forse l’andamento più curioso della velocità l’abbiamo con la lenza con doppia rastremazione, la enza più comunemente usata per questo tipo di lancio. Come si può vedere in Fig 5, la lenza con doppia rastremazione inizialmente decelera quando la porzione centrale del livello è srotolata. Appena la porzione conica entra nel loop, la lenza accelera abbastanza bruscamente. Questa accelerazione è velocemente sostituita da una fase di decelerazione persino più brusca fino a che si è raggiunta la velocità finale. Questo andamento della velocità dimostra sia un minimo che un massimo locali intermedi rispetto ai punti finali, ritrovamento che non era stato anticipato dall’analisi non viscosa. La distinta massimizzazione della velocità vicina,ma non “giunta a”, alla fine del lancio spiega il caratteristico “calcio” che i pescatori attribuiscono a questa lenza che spinge una mosca folta dietro la fine della lenza e, in termini di pescatori, “porta sopra il leader”. Dato che la rastremazione di questa lenza si è evoluta dopo molti anni di test “prova ed errore”, ci sono senza dubbio alcuni benefici del lancio associati con questo andamento della velocità. Una quantificazione numerica di questo beneficio è difficile questa volta.
La figura 5 mostra che ognuna delle 4 lenze analizzate richiede una diversa velocità iniziale per produrre la velocità finale desiderata di 30 m/s. la lunga lenza rastremata richiede la velocità iniziale più piccola, la lenza con doppia rastremazione la più grande.
Comunque, l’energia cinetica iniziale delle lenze non è parallela alle rispettive velocità perché la massa della lenza varia. Solo i primi 9.14m (30 piedi) di ciascuna lenza contengono uguale massa, la lenza rimanente deve essere usata per i 20 m di lancio ed ha una massa che varia con le rispettive rastremazioni. Quindi, come indicato in Tabella 1, l’energia iniziale per la lenza di livello è circa solo un mezzo di quella della lunga lenza rastremata. La lenza rastremata sperimentale richiede anche relativamente poca energia cinetica. L’energia iniziale della lenza è di vitale importanza per il pescatore dato che egli/ella sii deve nutrire con questa energia.; un lungo giorno di pesca rende una persona consapevole di quale sia una tecnica di lancio efficiente e dell’attrezzatura.
Questo modello separa gli effetti dell’attrito dell’aria in quelli che compaiono nel loop, la lenza che si muove e la mosca.
Fig. 6 Effetti del diametro del loop sulla lenza.
Di queste, l’attrito sul loop domina totalmente la complessiva perdita viscosa dell’energia meccanica. L’attrito sulla lenza che si sposta può essere più grande di quello sul loop quando la lenza che si muove è lunga, ma decresce continuamente con il progredire del lancio e l’accorciamento della lenza che si muove. L’attrito del loop rimane costante, e l’effetto integrato sulla durata del lancio enfatizza l’attrito del loop. Ciò è illustrato in Fig. 6, dove lo stesso lancio è modellato con differenti diametri di loop. L’iniziale velocità della lenza serve per consentire i 30 m/s della velocità della mosca al completamento del cast,aumenta bruscamente quando il diametro del loop aumenta per tutte le rastremazioni della lenza. La lenza di livello e quella sperimentale rastremate mostrano una dipendenza rispetto agli altri due, ma per tipici diametri di loop ci sono meno di 2m, la differenza è insignificante. Gli insegnanti di lancio ammoniscono costantemente i loro studenti affinché imparino le tecniche di controllo del loop, e sembra che le loro parole siano ben ascoltate. È fisicamente impossibile lanciare un loop di diametro zero, a causa dell’inerente rigidità nel flettersi della lenza e,ancora più importante, il superamento inerziale della punta della canna durante il lancio. Ma il vantaggio di un loop che è tanto piccolo quanto possibile è ovvio e drammatico.
V. CONCLUSIONI
Un modello dinamico di un tipico lancio con la mosca è stato sviluppato ed utilizzato per prevedere l’andamento della velocità della mosca e la porzione che si sposta della lenza quando la mosca è indirizzata verso un bersaglio specifico. Il modello indica i seguenti risultati:
(1)In assenza dell’attrito dell’aria,la mosca accelera continuamente durante il suo volo perché la massa della lenza che si muove decresce continuamente, richiedendo che la velocità aumenti per conservare l’energia cinetica.
(2)L’attrito dell’aria ha un effetto che incide pesantemente sull’andamento della velocità della mosca, causando diverse fasi di accelerazione e decelerazione che dipendono dalla rastremazione della lenza. E’ possibile selezionare una lenza rastremata che produca accelerazione pari a zero al completamento del cast
(3)L’attrito dell’aria sul loop che si forma tra la porzione di lenza che si muove e quella stazionaria domina del tutto l’effetto viscoso. Minimizzando il diametro del loop il pescatore può ridurre significativamente il totale di energia iniziale che deve essere impartita per completare il lancio
1E. Moser e W. W. Buchman, Flyfisher 13 (4), 5-9 (1980)
2S. Fry “Dinamica di un lancio con la mosca” (non pubblicato)
3D. Le Breton, “Principi e dinamica del lancio, V1 & V2”(non pubblicato)
4R. Terrill, Flyfhishing the West 4(2), 62-65 (1981)
5B. Bernstein, D. A. Hall and H.M Trent, J.Acoust, Soc Am 30 (12),1112-1115 (1958)
6O.S.F.Zucker e W.H. Bostick “Aspetti teorici e pratici della conservazione e della compressione dell’energia”, Proceedings of the International Conferente of Energy Storage,Compression and Switching.Asti,Torino,Italia,1972 (Plenum,New York, 1976) pp 71-93
7F.M. White, J. Basic Eng. 94 (1), 200-206 (1972)