BED-Vol. 50, 2001 – Conferenza di Bioingegneria – ASME 2001
ANALISI NUMERICA DELLA MECCANICA DEL LANCIO
Caroline Gatti, N. C. Perkins
Ingegneria Meccanica Università del Michiga – Ann Arbor, MI
Traduzione Barbara Panizzolo
INTRODUZIONE
La pesca a mosca differisce in modo significativo dalle altre forme di pesca sportiva in gran parte dovute ad apparecchiature che impiega il pescatore. Nella pesca a mosca,il pescatore getta una mosca artificiale leggera utilizzando il peso distribuito della lenza. Il movimento della lenza è controllata in parte dal movimento della canna a mosca (cioè,dal pescatore), così come da altre forze tra cui la resistenza dell’aria, la gravità e la tensione della lenza. L’azione del lancio è
ottenuta mediante un’onda non lineare, semplicemente denominata loop, che si propaga lungo la linea. In definitiva, questo loop raggiunge la fine della lenza dove si srotola vicino alla superficie dell’acqua.
Al contrario,nella rotazione o nellla pesca con esche, un pescatore getta un richiamo / esca / peso che ha un peso significativo rispetto alla lenza a cui è allegato.
In questo caso, la lenza leggera rimane in gran parte dritta ed è semplicemente tirata da una bobina in tensione.
La maggior parte dei pescatori richiede pratica considerevole per lo sviluppo di professionalità nel lancio. L’enorme quantità di pratica necessario per sviluppare con abilità tecniche di lancio sottolinea la meccanica sottile coinvolta nel lancio di una lenza. Solo un numero limitato di articoli tecnici ha
affrontato la fisica di base della lenza durante il lancio e questi sono anche contenute in una bibliografia disponibile su un sito web da parte di Spolek [1]. Di questi, tre pubblicazioni [2-4] sono più direttamente connesse a questo studio in quanto introducono i vari modelli della lenza.
In [2], Spolek introduce un modello idealizzato della lenza per un lancio sopra la testa prescrivendo la geometria della lenza. Così, la cinematica della lenza è determinata a priori dividendo la lenza in tre
segmenti. Un segmento rettilineo orizzontale inizia sulla punta della canna ed è collegato a un segmento semi-anello circolare che è poi collegato a un
segmento rettilineo finale orizzontale. Un equilibrio lavoro-energia è utilizzato per lo studio della propagazione del loop ideale semicircolare. I risultati di questo bilancio energetico evidenziano gli effetti chiave causati dalla rastremazione della lenza e dalla resistenza dell’aria sul segmento di loop. Un modello di attrito raffinato è stato successivamente proposto in [3]. In [4], Robson rilassa la cinematica vincolata in [2] ed introduce una approssimazione multi-corpo della lenza. La lenza è modellata come una sequenza di piccole particelle collegate da aste rigide e senza massa. Le canne sono collegate e quindi i relativi angoli articolari sono introdotti introducendo ad un grande livello-di-
libertà concentrato nel modello parametrico. Il movimento della punta della canna a mosca
è prescritto come l’input di questo modello che viene poi utilizzato per simulare la risposta della lenza sotto l’azione della gravità e dell’attrito. La geometria della lenza prevista dalla simulazione è in buon accordo con
ciò che è stato catturato nelle immagini video.
L’obiettivo di questo documento è di promuovere la fondamentale comprensione della meccanica del lancio. Un modello matematico di lenza sarà presentato ed utilizza allo stato d’arte modelli continui presi dalla zona della dinamica dei cavi. Questo modello continuo evita l’ipotesi di modellazione inevitabile introdotta in parametri concentrati in modelli e permette anche di prescrivere direttamente importanti proprietà fisiche della lenza tra cui il cono e la massa non uniforme. Soluzioni numeriche di questo modello sono discusse e rivelano come un loop si forma e si propaga lungo la lenza. Come recentemente sottolineato da Phillips [5], il settore pesca a mosca può essere in grado di capitalizzare tali simulazioni a computer di lancio come mezzo per comprendere e migliorare le prestazioni di lancio delle canne a mosca e delle lenze.
MODELLO E SIMULAZIONE DELLA LENZA
In questa presentazione, si inizierà con la modellazione di una lenza come un uni-dimensionale elastico continuo che è in grado di sostenere la tensione e la flessione. In sostanza, la lenza viene considerata come una molto sottile (non uniforme) canna a cui è consentito arbitrariamente subire deformazioni durante il lancio. Un elemento di questa lenza, considerato come un corpo libero, è soggetto al peso,alla resistenza dell’aria, ed alle tensione inerziale,al taglio ed a momenti di piegatura. Le equazioni del moto di questo elemento verranno presentate insieme alle leggi costitutive della lenza. Le equazioni risultanti di movimento costituiscono un problema non lineare iniziale con valore limitato. Le condizioni di contorno sono selezionate per descrivere l’estremità libera della lenza (fuga taglio e momento) e l’attaccamento alla punta della canna (Velocità prescritta momento di fuga). Le condizioni iniziali sono selezionate per rappresentare un perfetto “cast all’indietro” come descritto di seguito.
Soluzioni numeriche delle equazioni del moto sono perseguite a seguito di una strategia costituita da tre fasi simile a quella in [6]. Il primo passo è quello di discretizzare in tempo usando differenziazione all’indietro e risulta in un problema non lineare con valore limitato nello spazio. Il problema non lineare di valore limitato viene quindi linearizzato attraverso un’espansione di una serie di Taylor delle equazioni di campo del primo ordine. Infine, questo linearizzato problema del valore limitatosi trasforma in un problema lineare iniziale di valore (in spazio), che viene risolto esattamente. Gli ultimi due passaggi sono poi ripetuto fino ad un criterio di convergenza che è soddisfatto La strategia di soluzione è quindi avanzate per il prossimo passo in cui l’originale problema iniziale non lineare di valore limitato viene aggiornato. La soluzione di convergenza si ottiene dopo aver perfezionato i due step spaziale e temporale.
RISULTATI
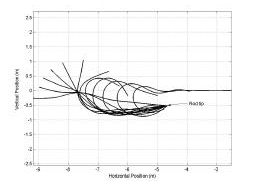
Figura 1. Simulazione di un lancio che mostra l’avvio e la propagazione di un loop a sinistra.
Il modello e metodo numerico descritto sopra è utilizzato per simulare la dinamica della lenza durante la fase di lancio in avanti di un lancio sopra la testa standard. La velocità della punta della canna, come rappresentato da condizioni di contorno, costituisce l’input del lancio e questo è stimato nel presente documento a misurazioni effettuate a partire da immagini video [7].
Le proprietà della lenza corrispondono a quelle di uno standard 5-peso, il peso in avanti, una lenza affusolata con una lunghezza variabile di lancio di 5 metri. Le condizioni iniziali di questa simulazione (non mostrate) descrivono la lenza idealmente lasciata orizzontalmente dietro al pescatore ed a riposo (a destra nella Figura 1). Queste condizioni iniziali descrivono un lancio perfetto all’indietro. A tempo t = 0, la fine della lenza collegata alla canna ci viene dato il prescritto movimento della punta della canna a mosca, e nelle ultime fasi del lancio, si forma un loop e si propaga verso sinistra come mostrato nella Figura 1. Figura 1 illustra la geometria della lenza (per 12selezionate volte) durante l’ultima fase del lancio in avanti quando la punta della canna è stazionaria.
Una comprensione fondamentale della formazione del loop e della sua propagazione può essere ottenuta dai dati mostrati nella
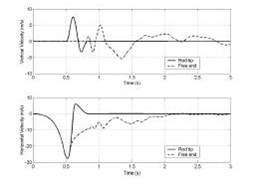
Figura 2. Questa figura illustra le componenti della velocità orizzontali e verticali della fine della lenza collegata alla punta della canna così come dell’estremità libera. L’ispezione di questa figura rivela che durante il primo mezzo secondo del lancio in avanti,le estremità della lenza hanno componenti della velocità identiche e che la punta della canna fa accelerare la lenza in direzione orizzontale. Così, nel corso di questo accelerazione iniziale, la lenza è quasi dritta sotto una tensione apprezzabile (e si comporta essenzialmente come un corpo rigido). Brevemente dopo 0.5 secondi, la punta della canna decelera rapidamente per fermarsi a circa 0.8 secondi. Durante questa decelerazione ed oltre, l’estremità libera della lenza ha una velocità che apprezzabilmente diversa da quella della punta della canna. Questa differenza di velocità è richiesta per la formazione di un loop. Infatti, la velocità di propagazione del loop cresce in proporzione alla differenza tra le velocità orizzontali alla punta della canna ed all’estremità libera.
Si possono anche derivare parametri quantitativi della prestazione del lancio da queste simulazioni ed utilizzarle per distinguere i disegni di mosche concorrenti. I parametri di lancio proposti includono la velocità del loop, il diametro del loop, la tensione del loop, l’energia dissipata dall’attrito dell’aria.
Questi parametri saranno utilizzati in questa presentazione per sviluppare ulteriormente la nostra comprensione della meccanica del lancio ed anche per valutare i vantaggi delle lenze affusolate come variabili primarie del disegno che influenzano la prestanza di un lancio.
Figura 2. Componenti della velocità delle estremità della lenza durante il lancio in avanti.
RINGRAZIAMENTI
Gli autori desiderano ringraziare l’assistenza tecnica e le forniture offerte dal signor Bruce Richards facente parte dei “Pescatori Scientifici”
RIFERIMENTI
1. Spolek, GA, http://www.me.pdx.edu/ graig ~ / cast-ref.htm
2. Spolek, GA, 1986, “La meccanica del lancio: La lenza”
American Journal of Physics, vol. 54, n. 9, pp. 832-835.
3. Lingard, S., 1988, “Note sulla aerodinamica di una lenza”,1988 “Journal of Physics, vol. 56, n. 8, pp. 756-757.
4. Robson, J.. M., 1990, “La fisica del lancio “, American Journal of Physics, vol. 58, n. 3, pp. 234-240.
5. Phillips, D., 2000, Tecnologia delle canne da pesca, Frank Amato Pubblicazione
6. Sun, Y., 1996, Modellizzazione e simulazione di distribuzione di bassa tensione oceanica cavo/corpo, Tesi di Dottorato, Università del Connecticut.
7. Krieger, M., 1985, L’essenza del lancio, video prodotto dal Club del Pacifico.