La fisica del Lancio

La Fisica del Lancio

John M. Robson^(a)

Dipartimento di Fisica, Sultan Qaboos University, Oman

(Ricevuta il 2 Marzo 1988; accettata per la pubblicazione il 24 Marzo 1989)

Traduzione Barbara Panizzolo

La fisica del moto in avanti del filo da pesca durante un lancio è discussa, ed è proposto un modello a computer di questo moto che riproduce le principali caratteristiche di questa parte del lancio.

1.INTORDUZIONE
Nella pesca a mosca il pescatore usa una canna di circa 3 metri di lunghezza per lanciare la lenza sull’acqua.

La lenza solitamente è lunga circa 10 m con un diametro di circa 1 mm ed una massa di circa 10 g. Una mosca artificiale è attaccata alla fine della lenza tramite un pezzo fine e leggero di mono-filamento chiamato leader.

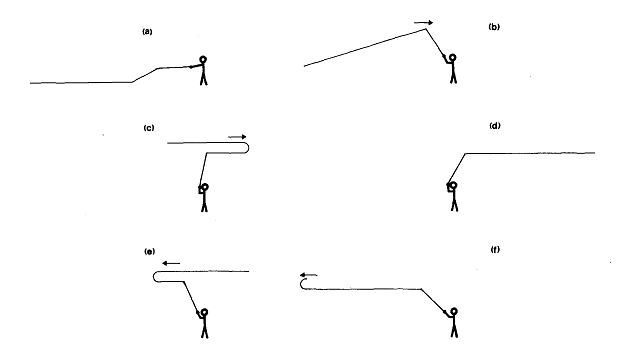
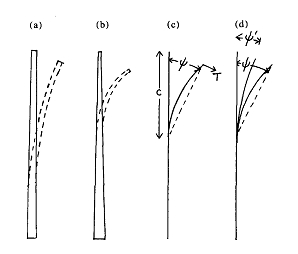
La massa del leader è solitamente di soli 300 mg e quella della mosca di circa 100 mg. Essi vengono portati avanti senza che compromettano gravemente il moto della lenza. Comunque, la forma e la lunghezza del leader influenzano il moto della mosca verso la fine del lancio. In un lancio completo, il pescatore alza la canna per sollevare la lenza fuori dall’acqua e per tirarla dietro di sé in modo che si raddrizzi approssimativamente parallela alla superficie. La canna è successivamente portata in avanti affinché la lenza si srotoli nell’aria e si depositi delicatamente sull’acqua. La sequenza è schematizzata nella Figura 1.

Molte variazioni di questa tipologia sono utilizzate dai pescatori, ma questa è la linea di movimento di base ed è quella di cui parleremo qui. Infatti, solo l’ultima parte,

Fig 1. Rappresentazione schematica del movimento della canna e della lenza durante il lancio con la mosca. La sequenza è nell’ordine da (a) verso (f)

il movimento in avanti della lenza, sarà trattato in modo dettagliato. È la parte più significativa del lancio ed incarna molti aspetti della fisica associata al moto della lenza. Innanzitutto, la fisica base del lancio sarà delineata nella Sezione II; ed un modello più dettagliato sarà usato nella Sezione III e sarà confrontato con i dati presi dai video dei lanci effettivi.

La meccanica di questo movimento in avanti della lenza e della mosca è stata trattata recentemente da Spolek¹. Egli sviluppa la fisica base  e la utilizza per calcolare la velocità della mosca durante il lancio. Egli mostra anche come questo dipenda criticamente dalla rastremazione della lenza. Il modello dettagliato presentato in questo articolo enfatizza l’effettivo forma della lenza durante il suo movimento così come la velocità della mosca.

II. SCHEMA DELLA FISICA DEL LANCIO IN AVANTI

A.Teoria basilare senza resistenza dell’aria

Si presume che il lancio in avanti inizi con la lenza interamente estesa all’indietro come mostrato in Fig 1 (d) ed istantaneamente al resto. La canna è portata avanti veloce per impartire una velocità in avanti ed un’energia cinetica alla lenza. È poi brutalmente stoppata affinché la lenza si raddoppi sull’estremità della mosca continuando in avanti come mostrato in Fig 1 (e) ed (f). Durante questo movimento, la canna inizialmente si flette all’indietro e poi si raddrizza dopo il brusco stop ed in questo modo la sua energia potenziale conservata è anche conferita alla lenza.

Per avere un’idea generale della fisica associata al movimento in seguito allo stop brutale, noi assumeremo prima di tutto che la canna non si fletta e che il brusco stop sia istantaneo. Con questa semplificazione la canna non compie lavoro sulla lenza dopo lo stop, sebbene eserciti una forza. Così se la resistenza dell’aria e la gravità sono trascurate, non è compiuto alcun lavoro dopo lo stop, e di conseguenza, l’energia cinetica della lenza rimane costante. Ciò nonostante, finchè la canna può esercitare una forza, il momento della lenza può decrescere.

Se z è la lunghezza della porzione della lenza che si sta ancora muovendo e v la sua velocità, l’energia cinetica dopo il brusco stop sarà

T= μzv²/2

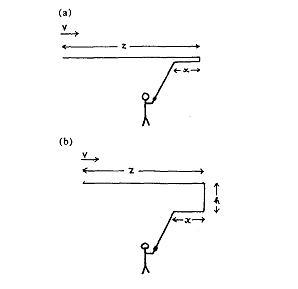
Dove μ è la massa per unità di lunghezza della lenza, che in questa semplice analisi si suppone essere uniforme nel diametro e nella densità. Inoltre, la massa della mosca è trascurata. La figura 2 (a) illustra la situazione. Dato che T è costante, la velocità è legata alla lunghezza della lenza, che si sta ancora muovendo con

v=(2T/ μz)^1/2 ,

e con momento

p=(2T μz)^1/2

Fig. 2 La canna e la lenza durante il lancio in avanti. Nell’ (a) il loop è molto stretto, mentre nella situazione più realistica (b), il loop rappresenta una frazione significativa della lunghezza della lenza. La teoria di questi due casi è spiegata nella sezione 2.

Quindi, la velocità aumenterebbe con il movimento in avanti della canna ed in questo caso idealizzato andrebbe all’infinito con il momento che tenderebbe a zero. La forza che accelera la parte in movimento della lenza è fornito dalla tensione nella lenza che, a turno, è opposta al tirare sulla sommità della canna.

Comunque, dato che la punta della canna è supposta essere stazionaria dopo il suo brusco stop, questo strattone non compie lavoro e non varia l’energia cinetica della lenza. Lo strattone si accresce quando z decresce e, infatti, sia la trazione che il suo impulso tendono all’infinito quando z tende a zero in questa semplificata teoria.

La frusta del cavaliere è stata analizzata in una maniera analoga da Rosenberg² , ma differisce nell’estremità, che corrisponde alla cima della canna alla fine della lenza da pesca, ed è mossa all’indietro ad una velocità finita. Perciò il lavoro è fatto sulla fursta dal cavaliere in contrasto con la situazione descritta qui.

B. Inclusione della resistenza dell’aria

L’effetto generale della resistenza dell’aria si può vedere da un’estensione di questa semplice teoria. La forma della lenza sarà adesso approssimata con la lenza in Fig 2 (b). Se l è la lunghezza totale della lenza e v è la velocità della mosca,

z + h + x = l

v = z – x = 2z

L’energia cinetica della lenza è

T = μzv²/2 + μhx²/2

= μ (4z + h) z²/2

Se il tempo t=0 si riferisce al momento di quando la canna si ferma bruscamente, l’energia cinetica a t = 0 è

T(0) = μ(l – h)V²/2

Dove V è la massima velocità di punta della canna poco prima che si fermi.

La forza della resistenza dell’aria sulla parte della lenza detta loop di lunghezza h sarà

Q = c_Drhp_az²

Dove c_D è il coefficiente di resistenza della linea di raggio r, e p_a è la densità dell’aria. La frizione della pelle è trascurata in questa semplice analisi. Di conseguenza, il lavoro fatto dalla lenza contro la resistenza dell’aria è

ò₀^x Qdx = – ò₀^t Q_z dt

quindi

T(0) – T = -ò₀^t c_Drhp_az³ dt,

e poi

m ( 4z + h)z² = 2 ò₀^tc_Drhp_az³ dt + T(0)

Il differenziale di questo ci da

(2m – c_Drhp_a)z² + (4z + h) mz = 0

Questa stessa equazione può essere ottenuta da Lagrange

L=T=2mzz² + mhz²/2

Se m ed h sono assunte come costanti, si ottiene la seguente equazione di moto

2mz² + ( 4z + h)mz = Q

dove Q è, come prima, la forza sulla lunghezza h dovuta alla resistenza dell’aria.

Dato che

d/dt (y^ky) = y^k-1 (ky² + yy),

la soluzione di questa equazione del moto esprime la velocità dell’estremità della lenza con la mosca come

v = 2z = c / (z + h/4)^k

dove

k = ½ – c_Drhp_a/4m

= ½ – (hp_a/4prr_l)c_D

dove r_l è la densità della lenza.

Quando x=0, z = l-h e v = V, la massima velocità della punta della canna poco prima di essere arrestata bruscamente è

C = V(l – 3h/4)^k,

quindi

v = V[´4l – 3h) / (4z + h)]^k

Di conseguenza, la velocità della mosca aumenterà o diminuirà durante il lancio dipendendo dalla positività o negatività di k. Il valore critico della misura del loop,

h_C è data da

h_C = 2prr_lc_D/r_a

Per una tipica lenza, il raggio è di circa 0.7mm ed h_c è di circa 200cm. Perciò, se il loop supera di circa 2m il lancio tende a collassare di fronte al pescatore.

La velocità massima v_m della mosca si verificherà quando z = 0, a patto che h < h_c :

v_m = V[ (4l – 3h)/h]^k.

Questo valore può diventare molto grande se h è piccola.

Nel lancio effettivo, la gravità e la curvatura della canna sono coinvolte così come la resistenza dell’aria. Queste inevitabilmente complicano la dettagliata descrizione della linea del moto e creano un’estensione di questa semplice teoria piuttosto difficile. Spolek, comunque, ha perseguito questo approccio ed ha sviluppato soluzioni numeriche dell’equazione risultante. In questo lavoro è stato sviluppato un modello alternativo, che sarà descritto nella Sezione III, che permette ragionevolmente di svolgere calcoli precisi con l’aiuto di un computer. Così dipende anche da soluzioni numeriche,  ma fornisce una visione alternativa sul moto durante il lancio.

III. UN MODELLO PIU’ DETTAGLIATO

1. Introduzione

In questa sezione è stato fatto un tentativo di estendere l’analisi includendo il fatto che la lenza non viaggia sempre su una linea diritta pulita, ma, come una bandiera mossa dal vento, ha delle ondulazioni nel suo moto. La gravità, il movimento dettagliato dell’estremità finale della canna con l’esca, e la curvatura della canna sono anch’esse incluse. Inoltre, sebbene la Sezione II trattasse solo il moto della lenza dopo l’arresto della canna alla fine del suo moto in avanti, questo modello tratterà l’intero lancio in avanti dal suo inizio in Fig. 1 (d) fino a che la lenza si ferma di fronte al pescatore.

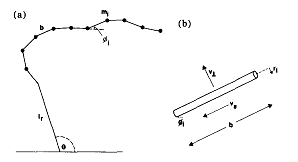
Fig. 3 (a) Il modello della lenza da pesca utilizzato nella maggior parte dei calcoli. La lenza è rappresentata come un numero di masse unite l’una all’altra da canne rigide rive di massa con perni privi di attrito localizzati su ciascuna massa. (b) Per introdurre la resistenza dell’aria, si presume che le canne prive di massa  abbiano dimensioni equivalenti a quelle della lenza. v₁ e v₂ sono le componenti della velocità perpendicolari e parallele alla lenza.

B. L’equazione del moto della lenza

È abbastanza semplice per definire l’esatta equazione del moto di una lenza continua soggetta alla resistenza dell’aria ed alla gravità che si muove attraverso l’aria. Questo è stato fatto da Wood³ che le ha usate per ottenere soluzioni approssimative per cavi trainati dietro ad aerei. Queste equazioni sono difficili da trattare,comunque, ed una rappresentazione più trattabile è stata utilizzata qui. È per rappresentare la lenza con un numero di n masse unite l’una all’altra con aste rigide prive di massa come mostrato in Fig 3 (a). Si presume che i perni localizzati sulle masse siano privi di attrito, ed il moto è limitato a due dimensioni. Un segmento individuale della lenza a cui ci riferiremo con il termine piccola linea, consiste di una massa m_i unita alla precedente massa m _i-1 da un’asta priva di massa di lunghezza b . La massa m_i è data da pr_i²br_l dove r_i è il raggio che una lenza continua avrebbe avuto alla posizione i-esima; r_l è la densità del materiale della linea continua. L’angolo che la i-esima piccola linea forma con il piano orizzontale sarà detto f_i.

Le coordinate x_i ed y_i della i-esima massa sono:

x_i =l_rcosq + å bcosf_k

e

y_i = l_rsinq + å bsinf_k

in questo modo l’energia cinetica e quella potenziale sono date da

2T = åm_i[(l_rsinqq +åbsinf_kfd_k)²

+ (l_r cosqq + å bsinf_kf_k)²],

V = åm_ig (l_rsinq + å bsin f_k).

Formando la regola di Lagrange ed utilizzando gli n angoli f_i come le coordinate, le equazioni simultanee in relazione a questi angoli risultano essere

a₁₁f₁ + a₁₂f₂ + … + a_1nf_n + a_1n+1 = 0

:            :                    :            :       :

:            :                    :            :       :

a_n1f₁ + a_n2f₂ + … + a_nnf_n + a_nn+1 = 0     (2)

Se trascuriamo la resistenza dell’aria ed assumiamo che la canna non si pieghi, i coefficienti sono

a_ij=B_ijcos(f_i – f_j), per j<=n

e

a_in+1=åB_ikf_k²sin(f_i – f_k) + Y_in+1

dove

B_ij = åm_k se i >=j oppure

åm_k se i<j

e

Y_in+1d = å m_k (l_r/b[qcos(q – f_i) – q²sin(q – f_i)] + (g/l_r)cosf_i)           (3)

L’angolo che la canna forma con la linea orizzontale è incluso nell’equazione (3) e q, che durante questi passaggi si riferisce all’angolo formato dall’estremità della canna come mostrato in Fig 3 e 4. Ora è necessario fare altre modiche per consentire la resistenza dell’aria e la curvatura della canna.

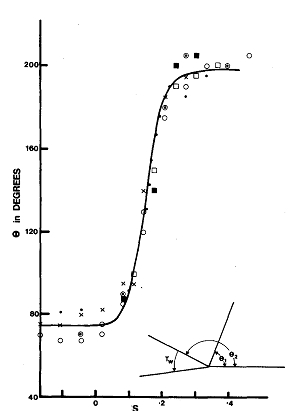
Fig. 4 Il moto della canna è descritto da q₁ e q₂, l’inizio e la fine previsti del lancio, un tasso di crescita dell’accelerazione angolare a tra q₁ e q₂ ed una costante di tempo legata al polso T_w che governa l’arresto finale dell’estremità della canna. Il grafico mostra i dati per più lanci con i punti che indicano gli angoli ricavati dalle registrazioni video.

Al fine di includere la resistenza dell’aria, la forza della pressione e la forza  dell’attrito della pelle su una piccola linea sono considerate come forze su un cilindro di lunghezza b e raggio r_i localizzato sull’ i-esimo tratto; vedere la Fig 3. Se v_^e v_// sono le componenti perpendicolare e parallela della velocità del tratto, le forze dell’i-esimo tratto sono

F_Di = r_ibc_Dir _av_^i |v_^i|,

e

F_Si = pr_ibc_Sir _av_//i |v_//i|,

dove c_Di è il coefficiente di attrito e c_Si è il coefficiente dell’attrito della pelle per l’i-esima linea. Quando questo è incluso, l’Eq 3 è modificata sostituendo l’ultimo termine m_k(g/l_r)cosf_i con

m_k(g/l_r)cosf_i – ( Q_Di – Q_Si)/l_r ,

dove

Q_Di = å F_Dk cos(f_i – f_k)

e

Q_Si = å F_Sk sin(f_i – f_k)

I coefficienti di DRAG dipendono dalla velocità della lenza e la seguente approssimazione è stata utilizzata per c_D in molti calcoli

c_D = 7.16  for R<1

c_D = 7.16R^-0.42 per 1<R<34

c_D = 3.02R^-0.165 per 34<R<1580

c_D = 0.9 per R>1580

dove R è il numero di Reynolds per il tratto ed equivale numericamente a 13.3v_ir_i dove v è in cm*s^-1 ed r_i è in cm. Questo algoritmo riproduce il manuale dato per un filo di forma cilindrica per numeri di Reynolds compresi tra 1 e 5000. Per il moto di una lenza da pesca, R è in questo intervallo per quasi tutto il lancio. L’attrito della pelle ha un effetto meno significativo sul moto e per semplicità il coefficiente d’attrito della pelle c_s si suppone avere il valore costante di 0.005. Un’espressione più dettagliata per questo coefficiente è stata data da Spolek e può essere usata come estensione di questo lavoro.

C. Il moto dell’estremità inferiore della canna

I differenti pescatori ovviamente usano differenti stili di lancio, ma una ragionevole approssimazione ad un normale lancio in avanti con una canna leggera ed una lenza sembra avere una un’accelerazione linearmente crescente seguita da una rapido decadimento esponenziale della velocità angolare dopo il brusco arresto. Sebbene un lancio sia descritto in questi calcoli con un angolo iniziale dell’estremità q₁ un tentato angolo di stop q₂ , un tasso di crescita dell’accelerazione angolare a tra questi angoli ed una costante di tempo di arresto T_w.

Tutto ciò e mostrato in Fig. 4. Sono anche mostrati alcuni punti sperimentali per q contro il tempo ottenuto da una registrazione video di alcuni lanci effettivi. La lenza solida è la posizione calcolata dell’estremità della canna per

a = 100 000°/s³ e T_w = 0.03 s

Le espressioni usate per q erano

q = q₁ + at³/6 per q < =q₂

e

q = q₂ + q₂T_w{1 – exp[-(t-t₂)/T_w]} per q>q₂

dove q₂ e t₂ sono valori di q e di t quando q=q₂ e sono date da

t₂ = {6(q₂-q₁)/a]^1/3 e q₂ = at₂²/2

D. La curvatura della canna

L’equazione (3) deve essere ulteriormente modificata al fine di tenere conto della curvatura della canna. Le canne per la pesca a mosca sono rese coniche in modo che il raggio all’estremità superiore sia minore del raggio dell’estremità inferiore; ovviamente, durante il lancio, essi si piega significativamente. Se il cono è piccolo, la canna si piegherà su molta parte della sua lunghezza, sebbene ci fosse un cono considerabile, la curvatura sarà localizzata più verso la punta come mostrato in Fig.5. La curvatura di una canna conica tramite un angolo largo può essere analizzata da un metodo simile a quello utilizzato da Timoshenko e Gere⁴ per canne uniformi e da Newman⁵per una corda flessibile, ma la teoria non lascia se stessa ad una semplice espressione analitica. Di conseguenza, in questo trattato del moto della lenza, la curvatura della canna durante il lancio è stato approssimato come mostrato in Fig 5. Si assume che la canna di lunghezza globale a si pieghi solo sopra una lunghezza c ed in un arco circolare sopra questa lunghezza. Inoltre si assume che l’angolo di deviazione, mostrato come Y nella Fig 5, sia proporzionale alla tensione sulla lenza  in cima alla canna. Di persè, questo dovrebbe dotare la canna con le proprietà di un semplice oscillatore armonico con una frequenza naturale w₀ legata al momento di inerzia I della porzione conica piegata ed alla deviazione per unità di forza d come segue:

w₀² = c² / Id

Le misurazioni sono state fatte su una particolare canna per la pesca a mosca e propongono questo valore di d=0.0007 cm dyn^-1, c=155cm ed I=1.2*10⁵ g cm² sarebbero appropriati. Questo ci da

w₀ = 16.9 s ^-1 o un periodo naturale di 0.37 secondi. Molti altre linee di canne differenti sono disponibili in commercio con periodi lunghi 1 secondo o corti come 0.1 secondi; questo particolare set di costanti è stato usato in questi calcoli.

Fig 5 Una canna con un piccolo cono è mostrata in (a) e si piega oltre la sua intera lunghezza, sebbene una canna con una conicità maggiore si pieghi solo sopra la parte superiore come mostrato in figura (b). In questo trattato si assume che la canna si pieghi su un cerchio su una lunghezza c come mostrato in (c). L’angolo lineare di deviazione Y è assunto come proporzionale a T, ma l’effettiva deviazione non lineare Y mostrata in (d) è stata calcolata da Y come descritto nel testo.

Il manico della canna di solito consiste in un manico in sughero incollato intorno alla parte più spessa della canna affusolata. Lo smorzamento della canna dipende da come questa impugnatura è saldamente afferrata dal lanciatore;di solito il grip è leggero durate il moto in avanti della canna seguito da un rapido serraggio quando il moto della canna viene fermato. In questi calcoli uno sottosmorzato coefficiente di 0,5 è stato utilizzato per il movimento in avanti con un coefficiente di 3,0 sovrasmorzato quando il lanciatore afferra saldamente l’impugnatura mentre cerca di fermare bruscamente il suo movimento.

Quando la canna è mossa da q₁ a q₂ è caricata dalla lenza ed il suo periodo naturale di oscillazione è perciò incrementato. Se la massa totale della lenza fosse stata m, si è assunto che la nuova frequenza angolare era data da

w² = c²/d(I + c² m)

Per un tipico lancio questo incrementa il periodo facendolo passare da 0.37 a 0.7 sec. Da questi numeri si può vedere che la lenza ha un effetto considerabile sulla risposta della canna.

La deviazione  della canna durante il moto in avanti è stata calcolata con una trasformazione standard di Laplace per una accelerazione at. Questo da

Y=a[wt – g + exp (-gwt/2)

* (gcosw₃ – fsinw₃t)]/w³ (4)

dove g è il coefficiente di smorzamento w₃=w(1 – g²)^1/2

ed f = (2 – g²)/(4 – g²)^1/2 » 0.9 per g=0.5

Quando il movimento in avanti della coda si ferma a q₂ si assume che il pescatore stringa l’impugnatura saldamente e che la deviazione della canna muoia lontano come se essa fosse sovrasmorzata con un coefficiente di smorzamento di 3.0.

Lo smorzamento della canna è solo lineare fino a circa 15° e poi diventa progressivamente sempre più non lineare.

Per consentire questo, una correzione dello smorzamento fu applicata utilizzando la relazione empirica

Y=Yexp(-bY),

dove Y è lo smorzamento effettivo corrispondente allo smorzamento lineare calcolata. Un valore di b=0.68 ci da un ragionevole accordo con gli smorzamenti sperimentali ottenute con la canna particolare ed è stato usato per molti calcoli.

Sebbene lo smorzamento durante il moto in avanti tra q₁ e q₂ sia probabilmente ben rappresentata dall’equazione (4), la semplice assunzione di un decadimento sovrasmorzato dopo che il movimento è stoppato è una considerabile semplificazione.

Si è ritenuto, comunque, che era giustificabile in questo trattato approssimato da quando il tiro della lenza è quindi approssimativamente nella direzione lungo la lunghezza della canna piuttosto che perpendicolare ad essa.

E. La procedura utilizzata nei calcoli

Per ottenere il moto della lenza, le coordinate della punta della canna e di ogni tratto sono state determinate a intervalli successivi Dt dall’inizio del lancio in avanti fino a t_m ,istante in cui la lenza era interamente estesa davanti al pescatore. Al fine di abolire le instabilità nelle soluzioni numeriche delle equazioni differenziali di second’ordine, il rapporto b/Dt, dove b è la lunghezza di ciascun tratto, deve essere tenuto più in considerazione di qualsiasi velocità che appare nel moto della lenza. Queste includono le velocità laterali analoghe a quelle che si verificano nel moto delle bandiere che sbattono al vento. La lunghezza b era generalmente tenuta a 30cm, che era il più grande valore i grado di non distorcere la forma della lenza. Un valore di Dt = 0.0001 s poi assicurò soluzioni stabili  e fu usato per molti calcoli.

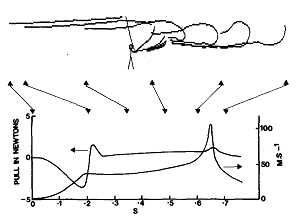
Fig.6Il risultato del calcolo per il lancio in avanti. La parte alta mostra la lenza nei tempi indicati dalle frecce che puntano all’estremità della mosca.Il grafico più basso mostra come la trazione della lenza sulla canna e la velocità della mosca vari durante il lancio. I dettagli del lancio particolare sono dati nel testo

Solitamente t_m era compresa tra 0.6 ed 1.0 secondi,una volta fatti 10000 per ogni lancio. Per ognuno di questi calcoli,gli angoli q ed Y sono stati ottenuti, ed il gruppo di equazioni simultanee mostrato nell’Equazione 2 sono state risolte per dare n valori di F_i. I valori di F_i e F_i dei precedenti calcoli sono stati usati per risolvere queste equazioni. I nuovi valori di F_i e F_i sono poi stati calcolati ed utilizzati per ottenere nuove coordinate cartesiane dei tratti e come input per il successivo gruppo di equazioni simultanee. Un tipico lancio impiega circa 6h su un PC IBM con un coprocessore matematico usando “IBM Professional FORTRAN”.

La figura 6 mostra il risultato ei calcoli per una lenza di livello di lunghezza pari a 900cm ed un raggio parti a 0.74 mm con il leader che si restringe da 0.45 a 0.1 mm su una lunghezza di 180cm. La mosca è stata approssimata con un cilindro di lunghezza 2cm e raggio 0.3 cm. L’estremità inferiore della canna è stata mossa da 75° a 155° con un tasso di aumento di accelerazione di 50 000° s^-3 e la costante di tempo di arresto del polso è stata considerata di 0.01sec.

I grafici mostrati sulla stessa figura indicano il tiro della lenza sulla canna e la velocità della mosca in funzione del tempo dall’inizio del lancio in avanti. Questo sarebbe visto come un lancio abbastanza buono da un pescatore in cui la mosca si è girata senza intoppi verso la fine del lancio senza avere una velocità eccessiva; c’è stato solo un leggero tiro sulla canna verso la fine del lancio, che sta ad indicare che non è stata spesa energia eccessiva nel moto della canna.

I valori più alti di accelerazione della canna vanno verso un sostanziale tiro sulla canna quando la canna si dispiega alla fine del lancio; ciò può essere usato per “tirare” lenza extra ed estendere il lancio, ma non porta ad una regolare presentazione della mosca.

F. Un test del modello

Al fine di testare interamente il modello, alcuni lanci sono stati registrati con una videocamera ad alta risoluzione e comparati con le previsioni del computer per lanci simili. È stato necessario utilizzare una videocamera con una risposta veloce per abolire la sfocatura dell’immagine sui frame individuali. Inoltre, un’ulteriore lenza pesante, un numero 9WF, deve essere usata per produrre una immagine facilmente visibile, e di conseguenza una canna è stata utilizzata e

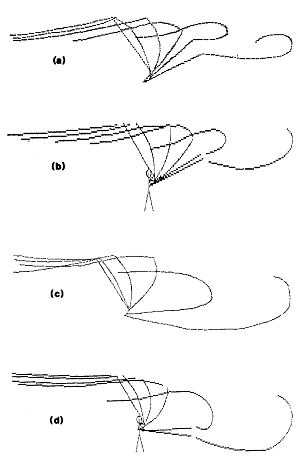
Fig 7 Due paragoni tra lanci effettivi registrati da una video camera e da previsioni a computer. (a) e (c) sono i lanci effettivi mentre (b) e (d) sono le simulazioni a computer. Per (a) e (b) la canna e la lenza sono mostrate a 0;0.16;0.32;0.44;0.64 e 1.0 s mentre per (c) e (d) i tempi sono stati 0;0.12;0.24;0.36;0.60 e 0.96 s.. Per dettagli della canna o dei movimenti del gomito fare riferimento al testo.

votata per il tipo di lenza;che misurava 3m di lunghezza. Con queste lenza e questa canna pesanti è stato scoperto che il moto della canna era meglio rappresentato da una piccola costante di accelerazione seguita da una velocità angolare uniforme; seguita da un decadimento esponenziale alla fine del lancio. Per aumentare il paragone, il programma è stato anche leggermente modificato per riprodurre il moto verso il basso del gomito durante il lancio.

La figura 7 mostra due paragoni tra i lanci effettivi e la loro simulazione a computer. Nel primo lancio è stata utilizzata una lenza corta, ed il lanciatore stava tenendo la lenza in aria senza abbassarla sull’acqua. (a) mostra la lenza effettivo e (b) la riproduzione a computer. Nel secondo lancio la lenza è stata abbassata sull’acqua; (c) è il lancio effettivo e (d) la riproduzione al computer. In vista della difficoltà di riprodurre i movimenti della canna con semplici approssimazioni usate nel programma,la convenzione è considerata abbastanza ragionevole.

IV.CONCLUSION

È stato mostrato che il moto durante il lancio in avanti di una lenza per la pesca a mosca  è approssimato da un sistema di energie cinetiche costanti. La resistenza dell’aria e la flessibilità della canna per la pesca a mosca portano delle modifiche ed introducono complicazioni che prevengono semplici soluzioni analitiche. Comunque, dal modello è stato presentato che è suscettibile a soluzioni di un piccolo computer e che riproduce i principali aspetti del movimento in avanti di una lenza per la pesca a mosca in ragionevole accordo con i lanci effettivi.

Si è soliti guardare nel modo in cui i lanci di pesca a mosca dipendono da varie caratteristiche della canna e della lenza e da diversi movimenti della canna. Queste sono in accordo generale con i risultati di Spolek e con l’esperienza effettiva, ma non sono riprodotte qui siccome sono di interesse maggiore dei pescatori piuttosto che dei fisici.

RICONOSCIMENTI

L’autore desidera ringraziare per l’aiuto fornito dal “Center for Educational Technology of Sultan Qaboos University” per i video degli effettivi lanci con la mosca e per aver fornito l’attrezzatura per il playback frame-by-frame. Desidera anche ringraziare il Dottor B.G. Newman per le molte discussioni utili ed informative sul moto delle bandiere e delle lenze.

^(a)Indirizzo permanente: Dipartimento di Fisica,McGill University, 3600 University Street, Montreal H3A 2T8, Canada

¹G.A. Spolek “La meccanica del lancio:La Lenza” Am J. Phys. 54, 832-836(1986)

²R.M. Rosenberg, “Dinamica analitica dei sistemi discreti” (Plenum, New York,1977), pp 332-334

³W.W.Wood, Rep A Laboratorio di ricerca aeronautica 122,Servizio Australiano di difesa scientifica, P.O.B. 4331 Melbourne, Victoria 3001,Australia (1961)

⁴S.P. Timoshenko e J.M. Gere, Teoria della stabilità elastica(McGraw-Hill,New York,1961) pp 76-82

⁵B.G. Newman, “Shape of a towed boom of logs” Proc. R. Soc. London Ser. A 346, 329-348 (1975)

Am. J. Phys., Vol. 58,No.3, March 1990                                                       John M. Robson 242